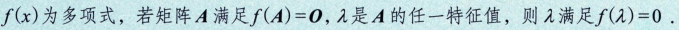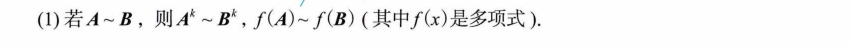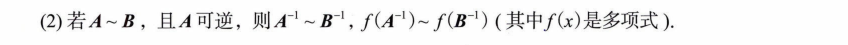一、行列式
1.
∣∣∣∣∣∣∣∣∣∣∣∣xbb⋮bbxb⋮bbbx⋮b⋯⋯⋯⋯bbb⋮x∣∣∣∣∣∣∣∣∣∣∣∣=[x+(n−1)b](x−b)n−1 .
若视 x 为变量, b 为常数,则行列式是 x 的 n 次多项式,其根是 x1=x2=⋯=xn−1=b,xn=(1−n)b .
当 a 取 λ−a 时, ∣∣∣∣∣∣∣∣∣∣∣∣λ−abb⋮bbλ−ab⋮bbbλ−a⋮b⋯⋯⋯⋯bbb⋮λ−a∣∣∣∣∣∣∣∣∣∣∣∣n×n=[λ−a+(n−1)b](λ−a−b)n−1 .
若视 λ 为变量, a,b 为常数,则行列式是 λ 的 n 次多项式,其根是 λ1=λ2=⋯=λn−1=a+b,λn=a−(n−1)b .
后续可求特征值
2.
①若行列式为 “X” 型,则
a. 主副对角线上元素相同.
∣∣∣∣∣∣∣∣∣∣∣∣∣ab⋱...abba...⋱ba∣∣∣∣∣∣∣∣∣∣∣∣∣2n=(a2−b2)n
b. 主副对角线上元素不同.
∣∣∣∣∣∣∣∣∣∣∣∣∣a1b2k⋱...akbk+1bkak+1...⋱b1a2k∣∣∣∣∣∣∣∣∣∣∣∣∣2k=i=1∏k(aia2k+1−i−bib2k+1−i).
当 2k=4 ,即 k=2 时, D4=i=1∏2(aia5−i−bib5−i)=(a1a4−b1b4)(a2a3−b2b3) .
以上两个公式通常用于后续矩阵的正定问题、二次型问题,而非只用于计算行列式.
②如类对称(主对角线元素相同,左下、右上各元素相同)行列式,可通过递推法、归纳法计算.
∣∣∣∣∣∣∣∣∣∣ac⋮cba⋮c⋯⋯⋯bb⋮a∣∣∣∣∣∣∣∣∣∣={[a+(n−1)b](a−b)n−1,b=c,b−cb(a−c)n−c(a−b)n,b=c.
③对于 n 阶行列式,记 Δ=k2−4bc ,有
∣∣∣∣∣∣∣∣∣kcb⋱⋱⋱⋱cbk∣∣∣∣∣∣∣∣∣n={(n+1)⋅(2k)n,k2=4bc,2n+1△(k+△)n+1−(k−△)n+1,k2=4bc
3. 克拉默法则简单推导
如何理解克拉默法则? - 知乎
就是通过构造一个这个样的矩阵:
xi=det⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛10⋮⋮⋮⋮⋮⋮00⋱⋱⋱⋮⋮⋮⋮⋯⋯⋱1⋱⋮⋮⋮⋮⋯0⋮010⋮⋮⋮0x1x2⋮⋮xi⋮⋮xn−1xn0⋮⋮⋮010⋮0⋯⋮⋮⋮⋮⋱1⋱⋯⋯⋮⋮⋮⋮⋮⋱⋱00⋮⋮⋮⋮⋮⋮01⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞
二、矩阵
1.
(ABC)⊺=C⊺B⊺A⊺
2. 二维下的旋转矩阵
M(θ)=⎣⎢⎡cosθsinθ−sinθcosθ⎦⎥⎤=cosθ[1001]+sinθ[01−10]=exp(θ[01−10])
[cosϕsinϕ−sinϕcosϕ][ρcosθρsinθ]=[ρcos(θ+ϕ)ρsin(θ+ϕ)]
3. 矩阵可逆的几个充要条件及其简要证明
矩阵可逆:
概念:对于 n 阶矩阵 A ,如果有一个 n 阶矩阵 B ,使
AB=BA=E
则说矩阵 A 是可逆的,并把矩阵 B 称为 A 的逆矩阵。
注意此处的可逆指的是方阵的逆,后面矩阵论中才会涉及到非方阵的广义逆矩阵或伪逆矩阵。
1. ∣A∣=0
充分性:
A A∗=A∗A=∣A∣E,
因 ∣A∣=0 ,故有
A ∣A∣1A∗=∣A∣1A∗ A=E ,
所以,按逆矩阵的定义,即知 A 可逆,且有
A−1=∣A∣1A∗
必要性:
证 A 可逆,即有 A−1 使 AA−1=E. 故 ∣A∣ ⋅∣A−1∣=∣E∣=1,所以 ∣A∣=0.
证毕。
2. A可表示为有限个初等矩阵相乘
充分性:
设A=P1P2⋯Pl,因初等矩阵可逆,有限个可逆矩阵的乘积仍可逆
必要性:
A 可逆⟺Q1⋯Q1A=B⟺A=Q1−1⋯Qi−1B=Q1−1⋯Qi−1E=Q1−1⋯Qi−1=P1⋯Pi
3. A等价于n阶单位矩阵
A 可逆⟺在可逆矩阵 P ,使 PA=E ⟺A∼ rE.
4. R(A)=n
R(A)=n⟺∣A∣=0⟺ 矩阵可逆
5. A的列(行)向量组线性无关
A的列向量组线性无关⟺对应齐次线性方程组只有零解⟺R(A)=n⟺ 矩阵可逆
6. 齐次线性方程组Ax=0仅有零解
7. 非齐次线性方程组Ax=b有唯一解
8. 任一n维向量可由A的列(行)向量组线性表示
9. A的特征值不为0
等价于∣A∣=0
4. 简单分块矩阵的逆
若 A,B 均是可逆方阵:
[AOOB]−1=[A−1OOB−1],[OBAO]−1=[OA−1B−1O]
副对角线分块矩阵的逆,可推广如下
A=⎣⎢⎢⎢⎡As...A2A1⎦⎥⎥⎥⎤,
其中 Ai(i=1,2,⋯,s) 可逆,则 A 可逆,且
A−1=⎣⎢⎢⎢⎡A1−1A2−1...As−1⎦⎥⎥⎥⎤.
若
A=⎣⎢⎢⎢⎡A1A2⋱As⎦⎥⎥⎥⎤,
则:
A−1=⎣⎢⎢⎢⎡A1−1A2−1⋱As−1⎦⎥⎥⎥⎤.
5. 一些伴随矩阵等式
A∗=∣A∣A−1,
∣A∗∣=∣A∣n−1,
(A∗)−1=(A−1)∗,
(A∗)⊺=(A⊺)∗,
(A∗)∗=∣A∣n−2A,
(AB)∗=B∗A∗,
(kA)∗=kn−1A∗.
6. 有关秩的一些式子
设A是m×n矩阵,B是满足有关矩阵运算要求的矩阵,则
①0⩽r(A)⩽min{m,n}(由定义)r(A)=0⇔A=O;
②r(kA)=r(A)(k=0)(由定义);
③r(AB)⩽min{r(A),r(B)};
④r(A+B)⩽r(A)+r(B);
⑤⋆ r(A∗)=⎩⎪⎪⎨⎪⎪⎧n,1,0,r(A)=n,r(A)=n−1,r(A)<n−1, 其中A为n(n⩾2)阶方阵;
用到了秩-零化度定理:dim(null(A))=n−rank(A)(该定理暂时不证明)

注意上述过程是等价的,也就是r(A)=n⇔r(A∗)=n,r(A)=n−1⇔r(A∗)=1,r(A)<n−1⇔r(A∗)=0.
⑥设A是m×n矩阵,P,Q分别是m阶n阶可逆矩阵,则r(A)=r(PA)=r(AQ)=r(PAQ);
⑦⋆ 若Am×nBn×s=0,则r(A)+r(B)⩽n;
⑧r(A)=r(AT)=r(ATA)=r(AAT).
三、向量组

1. 判别线性相关性的七大定理
定理 1 向量组α1,α2,…,αn(n⩾2)线性相关的充要条件是:向量组中至少有一个向量可由其余的n−1个向量线性表示。
其逆否命题:向量组α1,α2,…,αn(n⩾2)线性无关的充要条件是:任一向量都不能由其余的n−1个向量线性表示。
定理 2 若向量组α1,α2,⋯,αn线性无关而β,α1,α2,⋯,αn线性相关,则β可由α1,α2,⋯,αn线性表示,且表示法唯一。
定理 3 如果向量组β1,β2,⋯,βt可由向量α1,α2,⋯,αs线性表示,且t>s,则β1,β2,⋯,βt线性相关(以少表多,多的相关)。
其等价命题:如果向量组β1,β2,⋯,βt可由向量组α1,α2,⋯,αs线性表示,且β1,β2,⋯,βt线性无关,则t≤s。
定理 4 设m个n维向量α1,α2,⋯,αm,其中:
向量组α1,α2,⋯,αm线性相关⇔齐次线性方程组
[α1,α2,⋯,αm]⎣⎢⎢⎢⎢⎡x1x2⋮xm⎦⎥⎥⎥⎥⎤=x1α1+x2α2+⋯+xmαm=0
有非零解 ⇔r([α1,α2,⋯,αm])<m .
其等价命题:α1,α2,⋯,αm 线性无关的充分必要条件是齐次线性方程组只有零解.
向量组 α1,α2,⋯,αm 线性无关⇔ 只有全为 0 的 x1,x2,⋯,xm ,使 x1α1+x2α2+⋯+xmαm=0 成立
⇔[α1,α2,⋯,αm]⎣⎢⎢⎢⎢⎡x1x2⋮xm⎦⎥⎥⎥⎥⎤=0 只有零解
⇔r([α1,α2,⋯,αm])=m .
定理 5 向量β可由向量组α1,α2,⋯,αs线性表示
⇔ 非齐次线性方程组[α1,α2,⋯,αs]⎣⎢⎢⎢⎢⎡x1x2⋮xs⎦⎥⎥⎥⎥⎤=x1α1+x2α2+⋯+xsαs=β有解
⇔r([α1,α2,⋯,αs])=r([α1,α2,⋯,αs,β]).
反之则有,向量β不能由向量组α1,α2,⋯,αs线性表示⇔[a1,a2,⋯,as]⎣⎢⎢⎢⎢⎢⎢⎡x1x2⋮xs⎦⎥⎥⎥⎥⎥⎥⎤=x1a1+x2a2+⋯+xsas=β无解
⇔r([α1,α2,⋯,αs])=r([α1,α2,⋯,αs,β]).⇒r([α1,α2,⋯,αs])+1=r([α1,α2,⋯,αs,β])
定理6 如果向量组α1,α2,⋯,αm中有一部分向量线性相关,则整个向量组也线性相关.
其逆否命题:如果a1,a2,⋯,am线性无关,则其任一部分向量组都线性无关.
定理 7 如果一组n维向量α1,α2,⋯,αs线性无关,那么把这些向量各任意添加m个分量所得到的新向量(n+m维)组α1∗,α2∗,⋯,αs∗也是线性无关的.
其逆否命题:如果α1,α2,⋯,αs线性相关,那么它们各去掉相同的若干个分量所得到的新向量组也是线性相关的.
2. r(A+B)⩽r([A, B])⩽r(A)+r(B)


3. 若r(Am×n)=n(列满秩),则 r(Am×nBn×s)=r(Bn×s)
秩的上界:
对任意矩阵乘积AB有r(AB)≤r(B)。
理由:AB的行向量是B的行向量的线性组合,因此AB的行空间是B的行空间的子空间,故r(AB)≤r(B)
Sylvester 秩不等式:
对Am×n和Bn×s,有:r(A)+r(B)−n≤r(AB)代入已知条件r(A)=n,得:n+r(B)−n=r(B)≤r(AB)
结合以上两个不等式r(B)≤r(AB)≤r(B)
因此,r(AB)=r(B)。
补充Sylvester(斯尔维斯特) 秩不等式的证明:

该内容来自三个重要矩阵秩的不等式证明
四、线性方程组
向量组作为基础解系要满足的 3 个条件:⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧向量个数 s=n−r(A);线性无关;向量是方程组的解 .
1. 齐次方程组
①当r(A)=n (α1,α2,⋯,αn线性无关)时,方程组有唯一零解;
②当r(A)<n (α1,α2,⋯,αn线性相关)时,方程组有非零解(无穷多解),且有n−r个线性无关解.
2. 非齐次方程组
1. 有解的条件

2. 解的性质

3. 同解方程组

五、特征值与特征向量
补充 有理根定理
有理根定理
对于一些a0,...,an∈Z,如果P(x)=anxn+an−1xn−1+⋯+a0,p、q互质,且qp是多项式的根,则p是a0的因子,q是an的因子.
举例:
3x3−5x2+5x−2一定在符号下面表示的数字之中1.31.2 ,8个可能的答案:{1,2,31,32}
1. 特征值结论
①若 λ1,λ2,⋯,λn 是 A 的 n 个特征值,则
{∣A∣=λ1λ2⋯λn,tr(A)=λ1+λ2+⋯+λn.
实际上以三阶为例:

 ②
②



2. 常用特征值与特征向量



3. 相似矩阵
相似矩阵描述的是同一个线性变换,只是在不同坐标系下的表达.

性质:

结论:





注意这些都不能证明相似只是必要条件
可相似对角化的条件:




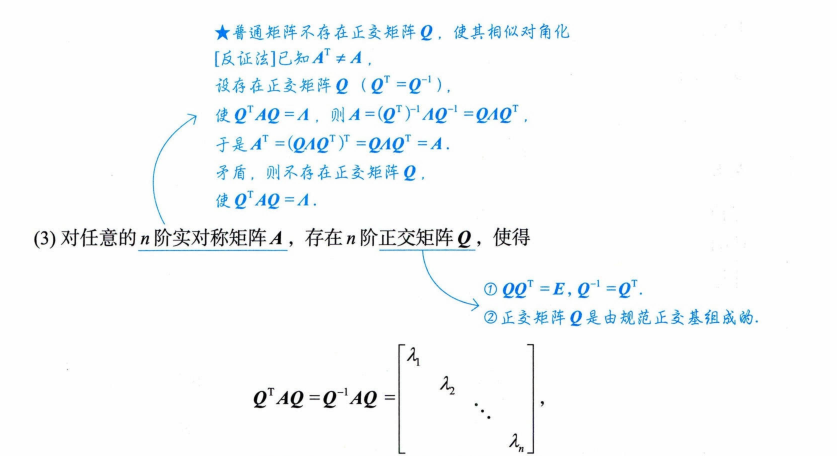
4. 实对称矩阵的相似对角化

注意这里描述有一点问题,实对称矩阵λ1=λ2时仍有可能ξ1与ξ2线性相关,只不过一定存在一组大小等于代数重数的线性无关特征向量,而普通矩阵并不具备这一特征(几何重数 < 代数重数的时候不可以对角化),可以由谱定理得到。
举个不可以对角化的例子:C=(51−13).
为什么实对称矩阵一定可以对角化?(拓展)

六、二次型
1. 合同
合同:A≃B或B=P⊤AP
等价:A≅B或B=QAP
相似:A∼B或B=P−1AP

2. 标准型与规范型定理
定理1 任何二次型 f(x)=xTAx 均可通过配方法(拉格朗日配方法作可逆线性变换x=Cy)化成标准型及规范型,用矩阵语言描述:任何实对称矩阵A,必存在可逆矩阵C,使得C⊤AC=Λ,其中:Λ=⎣⎢⎢⎢⎡d1d2⋱dn⎦⎥⎥⎥⎤,或Λ=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1⋱1−1⋱−10⋱0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
注:此处C的列向量一般不是A的特征向量,di(i=1,2,⋯,n)一般也不是A的特征值.
定理2 任何二次型f(x)=xTAx也可以通过正交变换x=Qy化成标准形,用矩阵语言表述:任何实对称矩阵A,一定存在正交矩阵Q,使得Q−1AQ=QTAQ=Λ,其中A=⎣⎢⎢⎢⎡λ1λ2⋱λn⎦⎥⎥⎥⎤.
注:此处Q的列向量均是A的特征向量,λi(i=1,2,⋯,n)均是A的特征值.
关于合同与对称矩阵的正交变换
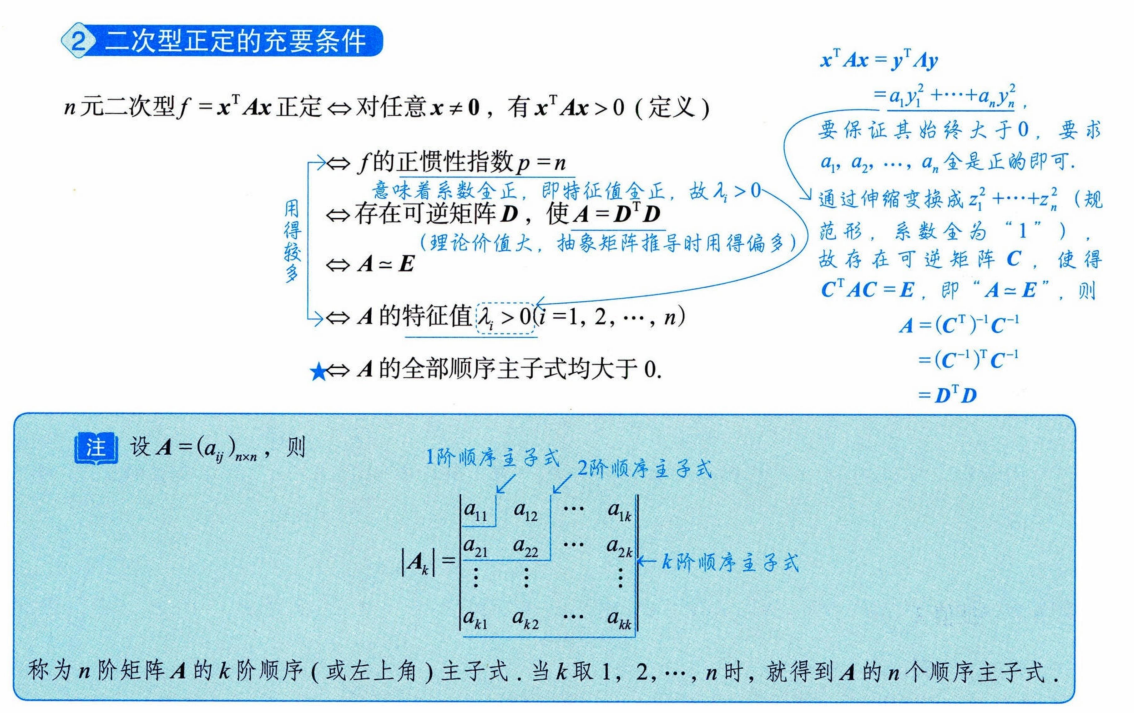
3. 正定二次型
一个矩阵是正定矩阵的前提是它是对称矩阵.

为什么顺序主子式大于零等价于正定?

A正定⇔A−1正定




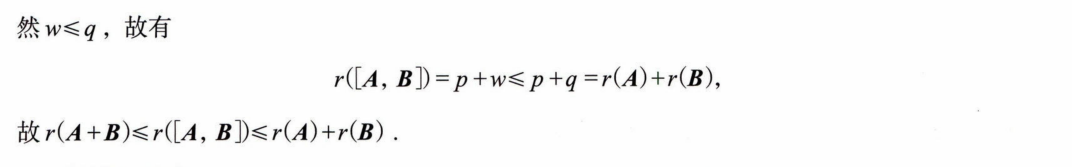




 ②
②